This blog post is about the GDR-Net: Geometry-Guided Direct Regression Network for Monocular 6D Pose Estimation paper which was published in CVPR 2021. The code for the proposed method is also freely available on github.
I am writing this paper review blog post as a part of my Master Seminar at TUM. You can also check out my presentation at this url. Authors of this paper have introduced a novel method for 6D direct pose estimation which is effectively end-to-end trainable and outperforms the state-of-the-art methods on LM, LM-O and YCB-V datasets.
Introduction and Problem Definition
Pose estimation is one of the most fundamental tasks in Computer Vision. Due to increased use of cameras in various fields such as robotics, autonomous driving and augmented reality, necessity of correct and effective estimation of camera-based object 6D pose has become more crucial. E.g. in robotics, most of the tasks such as object grasping, moving, fitting require a correct pose of the object to be known before taking further actions [1].
6D pose estimation of an object means defining its 3D rotation and 3D translation with respect to camera.
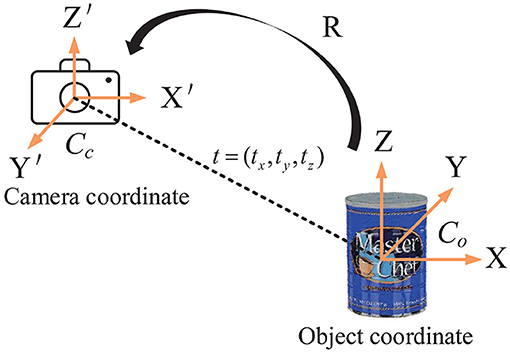
Rigid-body transformation of an object from a world coordinate to camera coordinate is implemented with a linear affine transformation matrix as follows. Please note that, there exist many different methods as well (quaternions, angle-axis etc.) which may provide an advantage over Euler angle representations in certain applications.
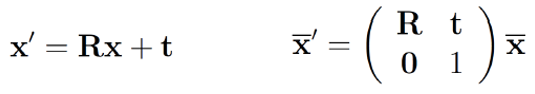
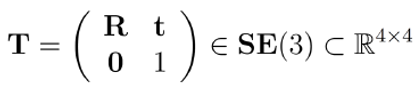
One of the challenges in pose estimation is ambiguity caused by visual appearance of an object. Hence, an object may seem very similar from different viewpoints. This is mostly due to occlusions, object symmetry, lack of textures or repetitive/symmetric patterns on the objects [2]. Consequently, more than one ground-truth pose exist for a similar view-point.
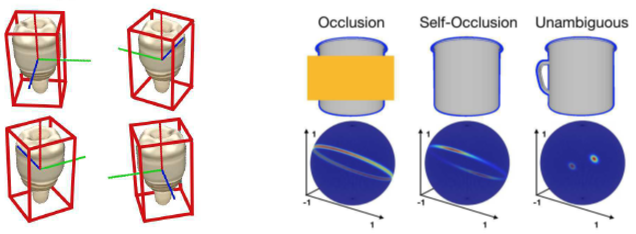
Pose ambiguity resulting from shape symmetry is an active research in shape analysis community and various non-DL based symmetry detection methods have been introduced to address this issue. E.g. [12] relies on edge feature extraction using Log-Gabor filter in different scales and orientations together with a voting procedure which is based on local color information.
Literature Review
Direct vs Indirect methods
In visual odometry, in order to estimate the camera pose, one of the 2D-2D, 2D-3D or 3D-3D point correspondences are established. Based on the chosen point correspondence method, one can estimate a camera pose based on either a reprojection or 3D geometric error function. Camera pose can be estimated with analytical methods as well [13].
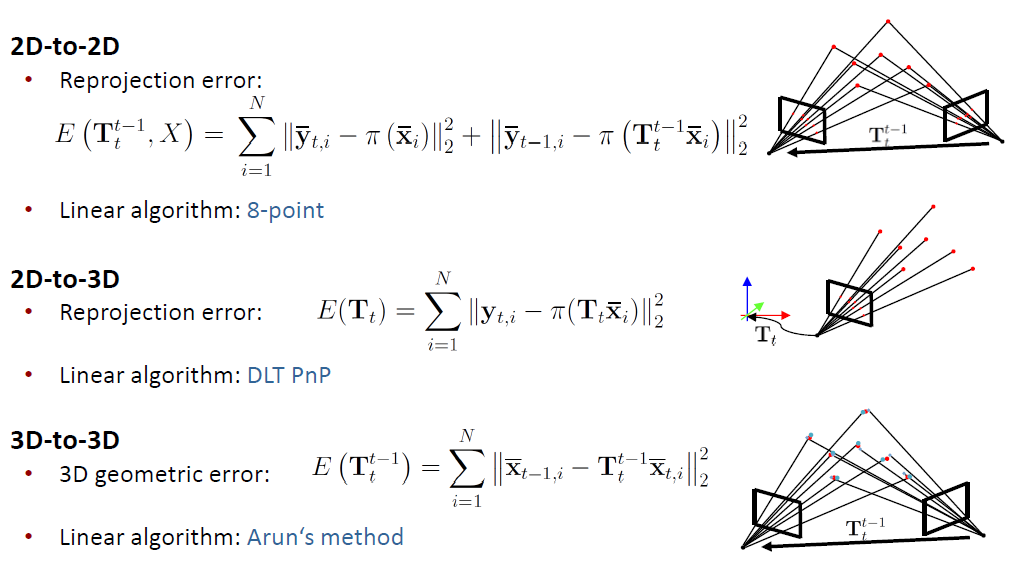
So, feature/keypoint extraction and matching is a very significant step in order to calcualate a pose of an object or camera w.r.t each other. There exist many methods for extracting as meaningful and unique features as possible such as SIFT, SURF, ORB, FAST, BRIEF etc. Even though these descriptors are often scale and/or rotation invariant, there still may be many feature mismatches due to the limits of feature extractors or feature matching metrics (matching distance). E.g. if we are too restrictive with our matching distance threshold, there might less true positives. On the contrary, if the threshold is more relaxed then there might more false positives.
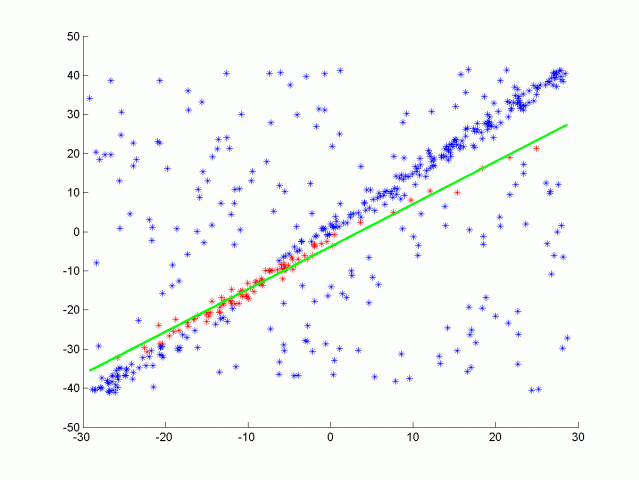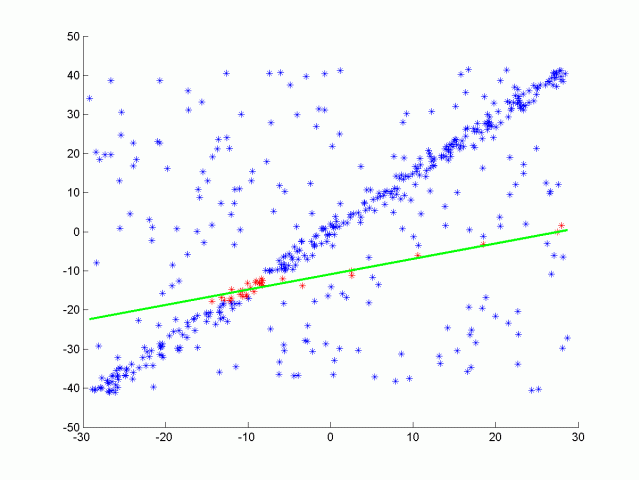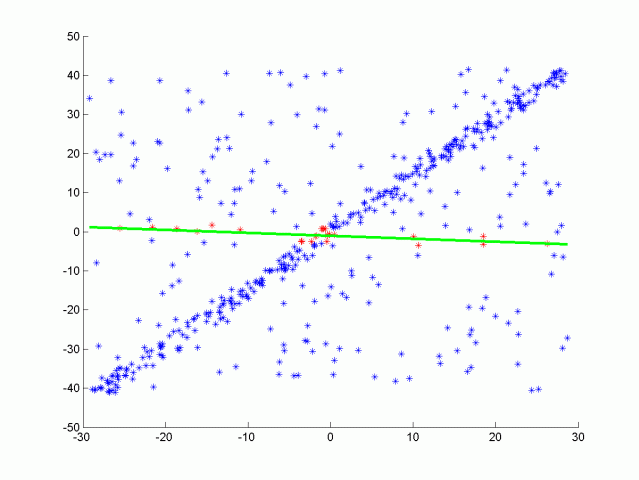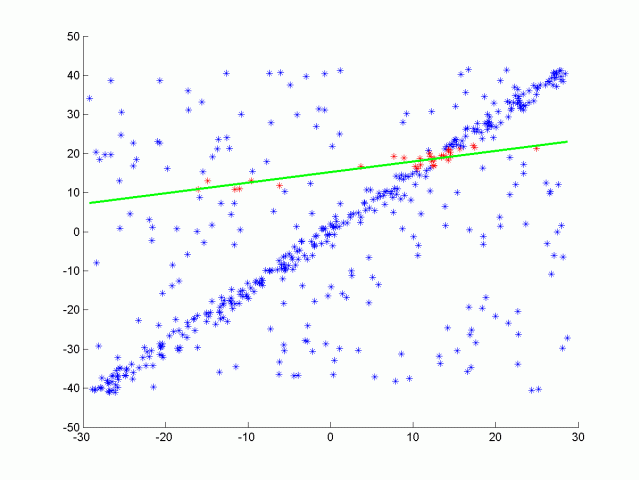
Random Sample Consensus (RANSAC)
RANSAC is an iterative method used to estimate the parameters of the mathematical model from given data points in the presence of outliers/noise (wrong correspondences). Basic idea of RANSAC is that at every iteration, algorithm randomly samples data points and tries to fit the model to these points. The goal is to find the best model that fits as many points as possible.
Using the following formula, it is possible to calculate the average number of iterations required to converge to the solution based on the certain hyperparameters such as probability of finding the correct solution (p), outlier-inlier ratio (ε), number of data points required for the solution (s) [13].
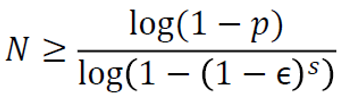
Perspective N-Point (PnP) Algorithm
PnP is a linear algorithm used to estimate the pose based on given 3D world coordinates of an object and a set of 2D corrosponding points in the image plane. Idea of the algorithm is to find a projective mapping which maps world coordinates to image pixel coordinates [15].
where transformation matrix is defined as follows:
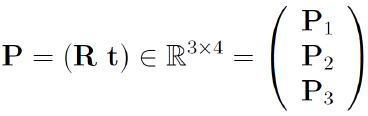
Transformation matrix can be found by solving the following linear equation.
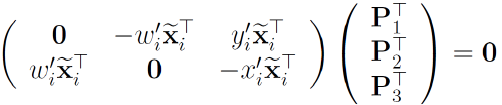
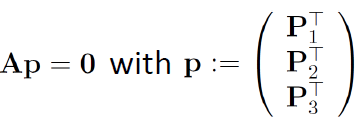
Matrix A has a rank of 8. Therefore, at least 4 point correspondences required for this linear system to be overdetermined and have a unique solution. However, in presence of outliers PnP can be subbject to errors, therefore it may be used in conjunction with an iterative methods like RANSAC. For example, [16, 17] uses a PnP algorithm to estimate the 6D pose of an object based on the corner points of bounding box which is detected using Convolution Neural Network (CNN).
Besides indirect methods, there also exist direct methods for pose estimation. As it can be from figure 5, direct methods perform direct image alignment by skipping the feature extraction and matching steps. This method usually requires the pixel depth to be known, therefore often uses RGB-D cameras which explicitly calculate the depth values too.
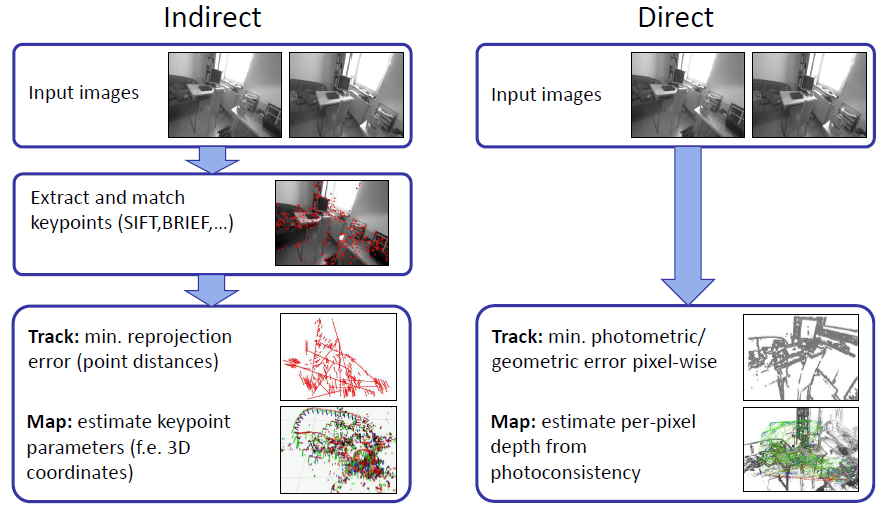
Generally, both of these traditional methods come with their own disadvantages. For instance, RANSAC/PnP algorithms can perform poorly on especially less textured or occluded objects. Additionally, as it is an iterative method, it can also be time consuming when dealing with dense correspondences. Therefore, in some applications PnP/RANSAC method is actually used as initialization method for more sophisticated non-linear optimization methods (e.g. Levenberg-Marquard). On the other side, depth camera based methods also have drawbacks due to limitations in resolution, field of view, range, frame rate and poor outdoor performance [18]. Additionally, depth cameras also cause quite significant battery drain as they are active sensors.
Besides traditional methods, there have been many Deep Learning (DL) based methods developed for pose estimation recently [16,17] and they have shown tremendous leap forward in accuracy and efficiency. Most of these methods use CNN based object detection, establish dense correspondence and then optimize the pose with a variation of PnP/RANSAC algorithm. However, there is major problem with this method as it is not differentable because the problem is usually decoupled into two separate steps. Some direct methods have also been proposed such as implementing backpropagation for PnP/RANSAC [21, 22], however these methods usually require very good initialization which may be hard to achieve.
Proposed Method
GDR-Net Architecuture Overview
In this paper, authors propose a novel way for establishing 2D-3D correspondences while computing the 6D pose in a differentable way. They also implement a new algorithm to learn PnP by assuming that the correspondences are in the image space because some of the previous methods ignored this fact, hence achieved poor results.
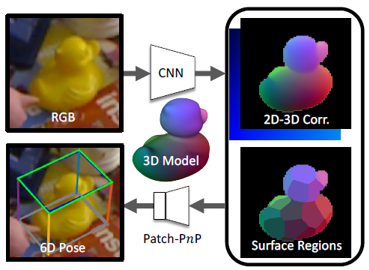
The goal of proposed method is to estimate 6D pose P = [R , t] with respect to camera for each object in the RGB image. Please, note that 3D CAD models for every object presented in the images are also available. R and t in the P pose matrix represent 3D rotation and 3D translation as mentioned early. The following figure demonstrates the general GDR-Net framework.
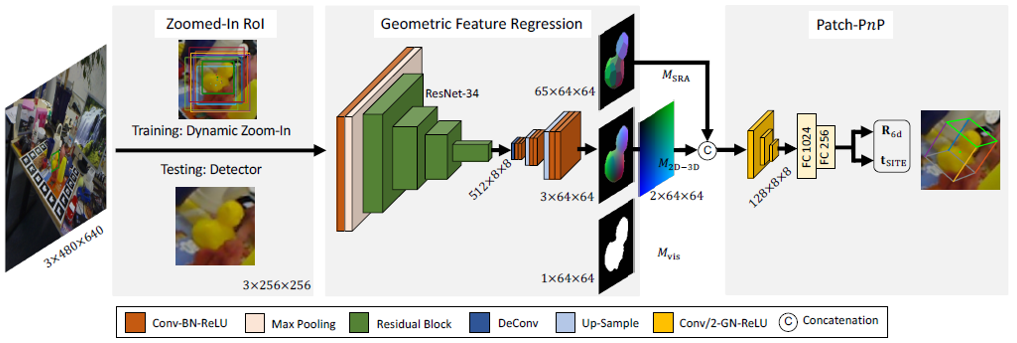
As it can be seen from the figure, the network consists of three main modules. In the first module, network accepts RGB image with the size of 480x640 and performs dynamic Zoom-In action for every object detected in the image. For object detection, authors use one of the off-the-shelf methods such as Faster R-CNN [23] or Fully Convolutional One-Stage Object Detector [24]. This allows us to decouple object detection problem from the pose regression and focus mainly on the 6D pose estimation while relying on the accuracy of a pre-designed detection algorithm. After detection, zoomed-in region, also called as Region of Interest (RoI), is passed to the neural network as an input in order to predict the intermediate geometric feature maps. In the final step, concatenated feature maps are passed to the Patch-PnP module, which uses fully connected layers to regress the 6D pose of an object. All in all, this paper illustrates relatively simple yet effective algorithm, which is a combination of regression-based direct and geometry-based indirect method, hence uses best of the both worlds. Before diving into more detailed structure of the GDR-Net, it is worth studying the specific parametrization this paper uses for the pose representation. Later in the ablation study, it will be shown that, this parametrization allows network achieve higher accuracy compared to more traditional parametrization methods.
Rotation and Translation Parametrization
As mentioned early, there exist various parameterization techniques to describe 3D rotation. Please note that it is generally easy to convert information from one representation to another. Some of these methods are ambiguous, i.e. there exist two different Ri and Rj (Ri != Rj) rotation matrices which may describe the same rotation. This is not desired for the neural network training, thus different methods such as unit quaternions or Lie algebra based methods are often used. According to [25], all 3D rotation representations with less than four dimensions have discontinuity in real Euclidean spacee. Consequently, when regressing rotations close to discontinuities, error becomes very large, therefore representations like Euler angles are hard to learn by neural networks. This is particularly ill-suited for regression problems where the full rotation space is required. So, they proposed a new 6D representation for rotation in SO(3).
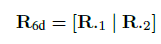
Given the 6D representation vector, R_6D = [r_1 , r_2], rotation matrix R = [R_.1, R_.2, R_.3] is calculated as follows:
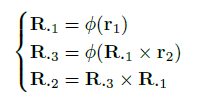
where φ(.) denotes to vector normalization. This representation has shown to be viewpoint-invariant under 3D translations, so, it is well-suited to deal with the zoomed-in RoI.
As direct translation t = [t_x ,t_y,t_z] regression does not work well in practice either, therefore translation is also decoupled into two parts: 2D location (o_x, o_y) of the projected 3D center of the object and the distance t_z between the object and camera. Some of the works actually estimate the 2D location as the center of the bounding box as well. Once we have 2D locations and distance from the camera, using intrinsics matrix we can estimate the 3D translation vector. However, because regressing (o_x, o_y) and t_z directly is not very suitable for especially zoomed-in regions, the authors utilize Scale-Invariant representaition for Translation Estimation(SITE) inspired from [3].
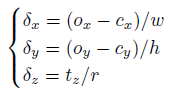
where, t_SITE = [δ_x, δ_y,δ_z]^T is scale-invariant translation vector, (w,h) are bounding box dimensions, (c_x, c_y) are object bounding box centers and r is the ratio of zoomed-in object size (max(h,w)) to normal object size.
6D Pose Loss
For 6D pose loss, authors have implemented a variant of Point-Matching loss which is based on the ADD(-S) metric (will be defined later). The purpose is to couple the estimation of rotation and translation. ADD(-S) used as a loss metric instead of simple distances such as L1 or L2.
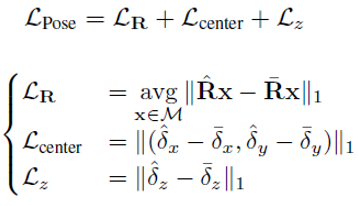
where ^ and - denote to prediction and ground truth,respectively.
Geometric Feature Regression and Patch-PnP
As previously mentioned GDR-Net framework consists of three main parts. Second part of the network is responsible for generating intermediate geometric features which are then passed to tghe third module, Patch-PnP. The first module of the network outputs an image of size 256x256 which is passed to feature extraction part and this part of the network extracts geometric features with spatial size of 64x64 composed of Dense Correspondences Map (M_2D-3D), Surface Region Atteention (M_SRA) and Visible Object Mask (M_VIS).
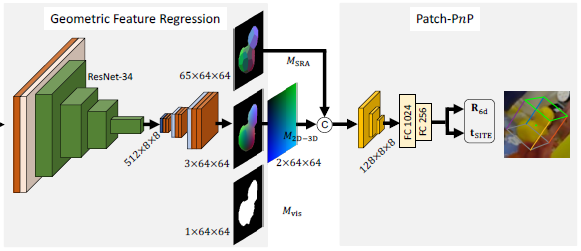
As can be seen from the figure, initially zoomed-in image’s spatial dimension are reduced to 8x8 using convolutional layer and ResNet-34. Then, the latent space is de-convolved and upsampled followed by convolutional layers. As a result, network reconstructs 64x64 image feature maps from the input. Even though, it is not illustrated in the figure, network actually estimates Dense Coordinate Maps (M_XYZ). M_2D-3D is then derived from stacking M_XYZ onto the 2D pixels. M_XYZ itself is obtained from rendering the 3D CAD model of the objects, hence, M_2D-3D (which is acquired from M_XYZ stack) also explicitly contains the shape information of the objects.
Another important geometric feature which is reconstructed as a network output is M_SRA. M_SRA contains the surface regions of the object and help us to deal with the ambiguities in the object shape. Ground-truth M_SRA is actually derived from Dense Coordinate Maps using farthest point sampling and it implicitly contains the object symmetry information. Unlike M_2D-3D, M_SRA is coarser representation of the object, hence it helps us to deal with the symmetry aware pose regression estimation. Therefore M_2D-3D is concatenated with M_SRA before being passed to the Patch-PnP module.
The Patch-PnP module consists of convolutional layers with kernel size of 3x3 and stride of 2 each followed by Group Normalization and ReLU activation. Two FC layers are applied to reduce the feature size from 8192 to 256. Eventually, two parallel FC layers output R_6d (parameterized rotation) and t_SITE (scale-invariant translation).
Geometric loss implemented in the paper is the sum of L1 loss for normalized M_XYZ and Visible Object Masks (M_VIS), and cross-entropy loss for M_SRA. Total loss for the GDR-Net is calculated as the sum of geometric and pose losses as follows.
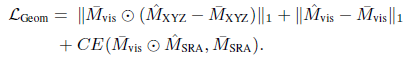
Experimental Setup and Results
Setup and Measurement Metrics
Neural Network was implemented using PyTorch library. Authors have used Ranger optimizer which is RAdam [26] optimizer combined with Lookahead [27] and Gradient Centralization [28] with batch size of 24 and a base learning rate of 1e-4. Experiments were conducted on Synthetic Sphere, LM, LM-O and YCB-V datasets. Two main metrics were used for evaluating the 6D pose: ADD(-S) and (n deg, n cm)
ADD metric measures if the average deviation of the transformed points are smaller than the 10% of the object’s diameter. ADD(-S) is a modification of ADD metric which is used for symmetric objects. It measures the average distance to the closest model point. Additionally, authors have used AUC (area under curve) of ADD(-S) for YCB-V dataset. (n deg, n cm) metric is also used in ablation study to measure whether the 3D rotation and translation errors are less than n deg and n cm, respectively.
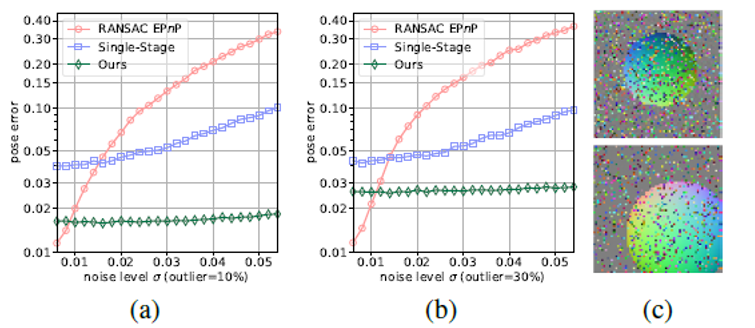
Synthetic Sphere Experiment Results
Purpose of this experiment was to compare the quality of Patch-PnP pose regression against more traditional PnP/RANSAC on Synthetic Sphere dataset. Following figure demonstrates the effectiveness of proposed Patch-PnP method. It can be seen that, Patch-PnP module’s output is much more consistent to random Gaussian noise than RANSAC/EPnP method as pose error remains almost unchanged while RANSAC/EPnP grows with the increased noise levels.
Ablation Study on LM (Quantitative)
Second study was an ablation study of GDR-Net on LM dataset. This is detailed study in order to show the clear advantage of GDR-Net architecture with its parameterization choices. GDR-Net was first run on LM dataset with default loss type (geometric + pose), and rotation and translation parameterization.
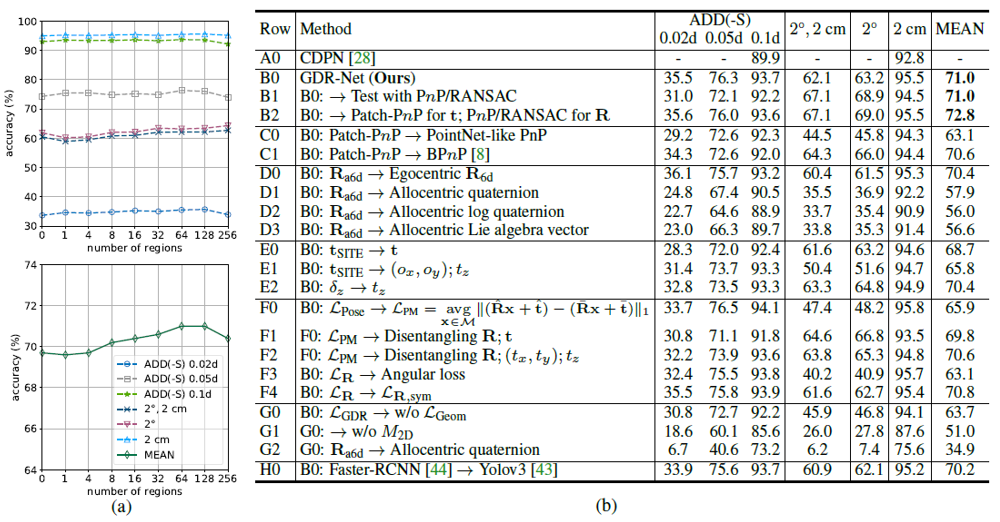
Figure shows that the best overall results are achieved for default architecture that have been proposed by the authors. Mean accuracy of GDR-Net with Patch-PnP is 72.8%. This accuracy actually goes down when PnP/RANSAC based pose regressor is used instead of Patch-PnP. Results also show that accuracy is significantly reduced when parameterization of 3D rotation is changed from proposed 6D vector representation to more traditional quaternion or Lie algebra based representation. Another notable result is that when network loss is used without geometric loss (only 6D pose loss), accuracy can reduce from 72% to 63.7%.
Comparison with SOTA (Quantitative)
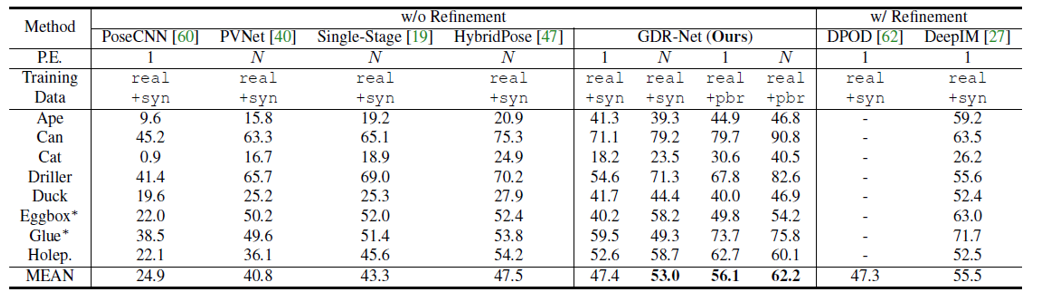
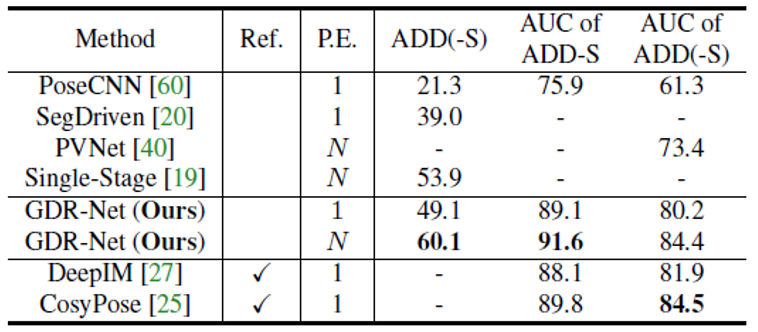
Following two figures illustrate further quantitative comparison of GDR-Net with SOTA methods on LM-O and YCB-V datasets. Both tables clearly show that our method significantly outperforms SOTA methods on both dataset when one pose estimator per object is used.
Qualitative Results



Conclusion
6D pose estimation has become one of the crucial topics in computer vision as cameras are getting used extensively in many applications. Recent trends show that every year more and more deep learning based solutions are introduced to tackle this challenging problem. Neural networks are either used partially to solve correspondence problem or provide direct, fully differentable solution. The paper introduced a novel way for 6D pose regression from a monocular camera. This method coupled the geometry based indirect method with direct method achieving an end-to-end trainable network. Extensive experiment results also demonstrated the it outperforms the SOTA methods on multiple datasets.
Even though, network was tested on LM, LM-O, YCB-V datasets, its performance on more challenging datasets (e.g. T-Less dataset) where almost all the objects are symmetric is still questionable from my point of view. Authors also have mentioneed in their conclusion that they want to extent their work to unseen object categories or harder scenarious with lack of annotated real data.
References
[1] Liang Guoyuan, Chen Fan, Liang Yu, Feng Yachun, Wang Can, Wu Xinyu. Frontiers in Neurorobotics. A Manufacturing-Oriented Intelligent Vision System Based on Deep Neural Network for Object Recognition and 6D Pose Estimation. https://www.frontiersin.org/article/10.3389/fnbot.2020.616775
[2] via Render-and-Compare. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 3559–3568, 2018Fabian Manhardt, Diego Arroyo, Christian Rupprecht, Benjamin Busam, Tolga Birdal, Nassir Navab, and Federico Tombari. Explaining the Ambiguity of Object Detection and 6D Pose From Visual Data. In IEEE International Conference on Computer Vision (ICCV), pages 6841–6850, 2019
[3] Zhigang Li, Gu Wang, and Xiangyang Ji. CDPN: Coordinates-Based Disentangled Pose Network for Real-Time RGB-Based 6 DoF Object Pose Estimation. In IEEE International Conference on Computer Vision (ICCV), pages 7678–7687, 2019.
[4] Yi Zhou, Connelly Barnes, Jingwan Lu, Jimei Yang, and Hao Li. On the Continuity of Rotation Representations in Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 5745–5753, 2019
[5] Kiru Park, Timothy Patten, and Markus Vincze. Pix2Pose: Pixel-Wise Coordinate Regression of Objects for 6D Pose Estimation. In IEEE International Conference on Computer Vision (ICCV), pages 7668–7677, 2019
[6] Sergey Zakharov, Ivan Shugurov, and Slobodan Ilic. DPOD: 6D Pose Object Detector and Refiner. In IEEE International Conference on Computer Vision (ICCV), pages 1941–1950, 2019
[7] Charles R Qi, Hao Su, Kaichun Mo, and Leonidas J Guibas. PointNet: Deep learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 652–660, 2017
[8] Eric Brachmann, Alexander Krull, Frank Michel, Stefan Gumhold, Jamie Shotton, and Carsten Rother. Learning 6D Object Pose Estimation Using 3D Object Coordinates. In European Conference on Computer Vision (ECCV), pages 536–551, 2014
[9] Gu Wang, Fabian Manhardt, Federico Tombari, Xiangyang Ji. GDR-Net: Geometry-Guided Direct Regression Network for Monocular 6D Object Pose Estimation. In CVPR 2021, June 2021.
[10] Yi Zhou, Connelly Barnes, Jingwan Lu, Jimei Yang, and Hao Li. On the Continuity of Rotation Representations in Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 5745–5753, 2019.
[11] Abhijit Kundu, Yin Li, and James M Rehg. 3D-RCNN: Instance-level 3D Object Reconstruction
[12] Mohamed Elawady, Christophe Ducottet, Olivier Alata, C´ecile Barat, and Philippe Colantoni. Wavelet-based reflection symmetry detection via textural and color histograms. ICCV Workshop, 2017.
[13] Niclas Zeller. Lecture 6: Visual Odometry 2: Indirect Methods, lecture notes. Robotic 3D Vision, Technical University of Munich, delivered on Winter Semester 2020/21.
[14] Niclas Zeller. Lecture 5: Visual Odometry 1: Indirect Methods, lecture notes. Robotic 3D Vision, Technical University of Munich, delivered on Winter Semester 2020/21.
[15] Richard Hartley, Andrew Zisserman (2003) Multi-View Geometry in Computer Vision, Second Edition edn., United States of America, New York: Cambridge University Press.
[16] Mahdi Rad and Vincent Lepetit. BB8: A Scalable, Accurate, Robust to Partial Occlusion Method for Predicting the 3D Poses of Challenging Objects without Using Depth. In IEEE International Conference on Computer Vision (ICCV), pages 3828–3836, 2017.
[17] Bugra Tekin, Sudipta N. Sinha, and Pascal Fua. Real-Time Seamless Single Shot 6D Object Pose Prediction. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 292–301, 2018.
[18] Yi Li, Gu Wang, Xiangyang Ji, Yu Xiang, and Dieter Fox. DeepIM: Deep Iterative Matching for 6D Pose Estimation. International Journal of Computer Vision (IJCV), pages 1–22, 2019.
[19] Model based Training, Detection and Pose Estimation of Texture-less 3D Objects in Heavily Cluttered Scenes. In Asian Conference on Computer Vision (ACCV), pages 548–562, 2012
[20] Frank Michel, Alexander Kirillov, Erix Brachmann, Alexander Krull, Stefan Gumhold, Bogdan Savchynskyy, and Carsten Rother. Global Hypothesis Generation for 6D Object Pose Estimation. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017
[21] Eric Brachmann, Alexander Krull, Sebastian Nowozin, Jamie Shotton, Frank Michel, Stefan Gumhold, and Carsten Rother. DSAC-Differentiable RANSAC for Camera Localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 6684–6692, 2017
[22] Bo Chen, Alvaro Parra, Jiewei Cao, Nan Li, and Tat-Jun Chin. End-to-End Learnable Geometric Vision by Backpropagating PnP Optimization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pages 8100–8109, 2020
[23] S. Ren, K. He, R. Girshick, and J. Sun. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Advances in Neural Information Processing Systems (NeurIPS), 2015
[24] Zhi Tian, Chunhua Shen, Hao Chen, and Tong He. FCOS: Fully Convolutional One-Stage Object Detection. In IEEE International Conference on Computer Vision (ICCV), pages 9627–9636, 2019
[25] Yi Zhou, Connelly Barnes, Jingwan Lu, Jimei Yang, and Hao Li. On the Continuity of Rotation Representations in Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 5745–5753, 2019
[26] Liyuan Liu, Haoming Jiang, Pengcheng He, Weizhu Chen, Xiaodong Liu, Jianfeng Gao, and Jiawei Han. On the Variance of the Adaptive Learning Rate and Beyond. In International Conference on Learning Representations (ICLR), April 2020.
[27]Michael Zhang, James Lucas, Jimmy Ba, and Geoffrey E Hinton. Lookahead Optimizer: k Steps Forward, 1 Step Back. In Advances in Neural Information Processing Systems (NeurIPS), pages 9593–9604, 2019
[28] Hongwei Yong, Jianqiang Huang, Xiansheng Hua, and Lei Zhang. Gradient-Centralization: A New Optimization Technique for Deep Neural Networks. In European Conference on Conputer Vision (ECCV), 2020
